Feature Selection Using Stochastic Gates (STG)
Feature selection problems have been extensively studied in the setting of linear estimation (e.g. LASSO), but less emphasis has been placed on feature selection for non-linear functions. This study introduces a novel feature selection method for neural network estimation, employing a probabilistic relaxation of the 0 norm to identify key features. Our approach, utilizing a continuous approximation of the Bernoulli distribution, enables simultaneous learning of nonlinear regression or classification functions, while identifying and utilizing only a limited subset of relevant features, through gradient descent.
Probabilistic Feature Selection Using Bernoulli Distribution
In probabilistic feature selection We employ Bernoulli gates for each input feature of the neural network, which are represented by a random vector with entries that follow a Bernoulli distribution. The probability that the gate for a particular feature is active is denoted by π_d, which transforms the combinatorial problem of feature selection into an optimization problem over these probabilities.
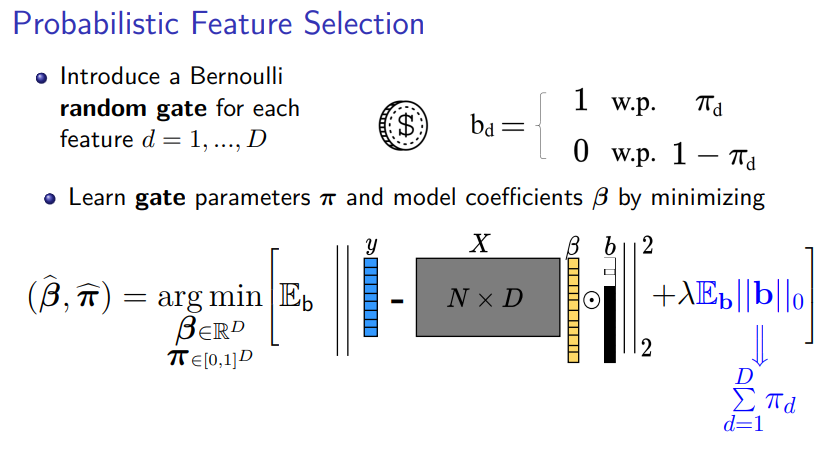
However, directly optimizing this probabilistic model is difficult due to the discrete nature of Bernoulli variables, which can introduce high variance in the optimization process.
Stochastic Gates (STG)
To solve this issue, we propose a Gaussian-based continuous relaxation of the Bernoulli variables, which we term stochastic gates (STGs). These gates can be visualized as clipped Gaussian distributions.
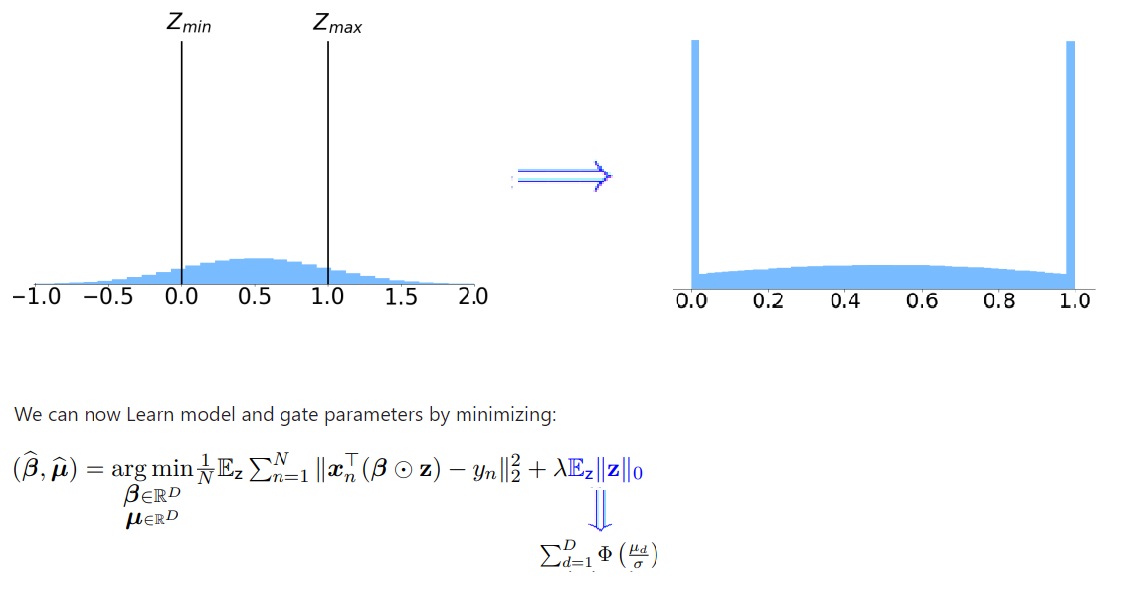
The STG is defined as z_d = max(0, min(1, µ_d + ε_d)), where ε_d is a noise term sampled from a Gaussian distribution, and µ_d is the gate’s parameter which controls the probability of the gate being active. Correspondingly, the regularization term aggregates the sum of the active gate probabilities, which are calculated using the standard Gaussian cumulative distribution function (CDF), Φ.
To optimize the feature selection model, we employ a Monte Carlo sampling-based gradient estimator. The gradient of the loss function concerning the gate parameters µ is combined with the regularization term’s derivative to update our model parameters efficiently using Stochastic Gradient Descent (SGD). After training, we can remove the randomness by setting the gate values based on their mean parameters to finalize the feature selection.
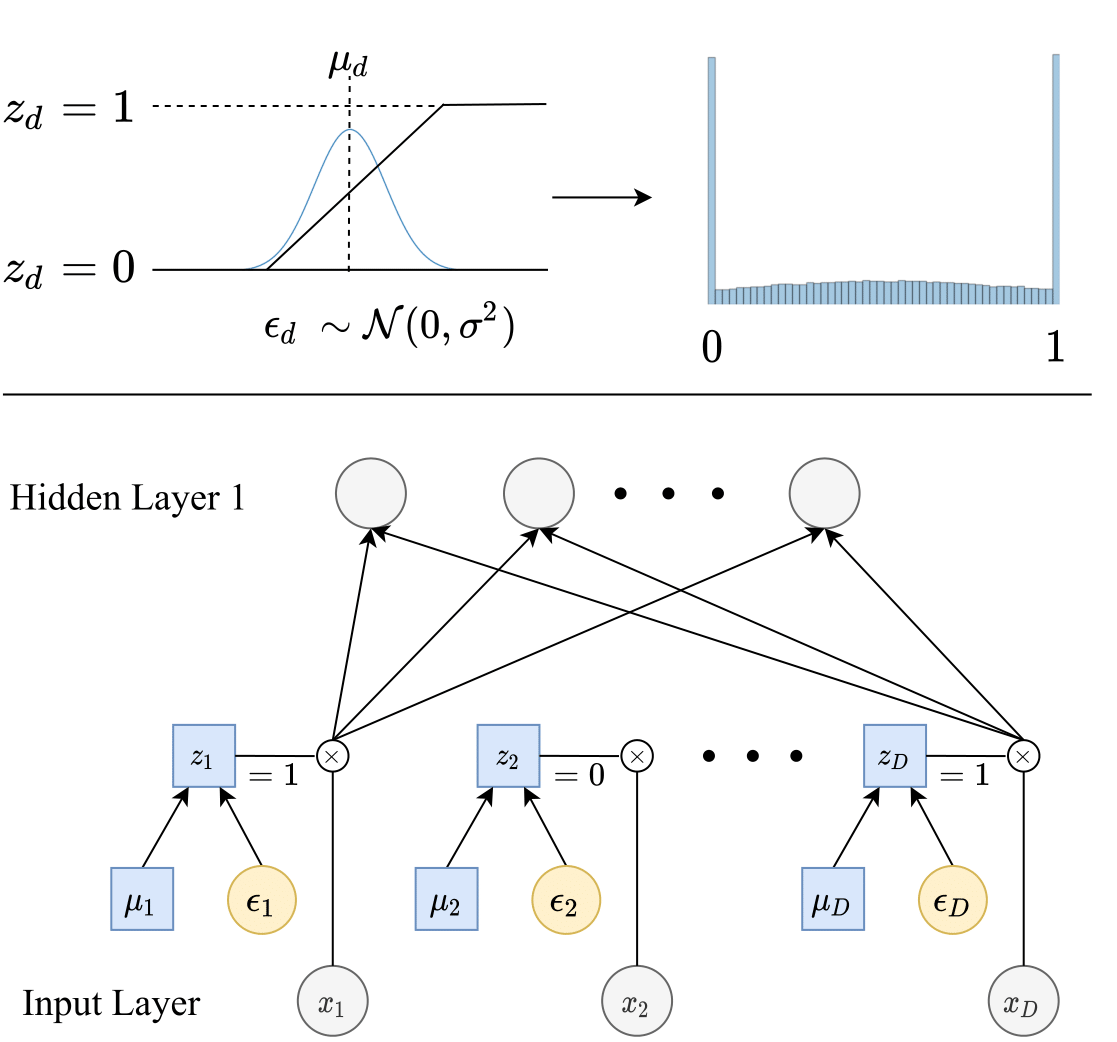
Top: Each stochastic gate z_d is drawn from the STG approximation of the Bernoulli distribution (shown as the blue histogram on the right). Specifically, z_d is obtained by applying the hard-sigmoid function to a mean-shifted Gaussian random variable. Bottom: The z_d stochastic gate is attached to the x_d input feature, where the trainable parameter µ_d controls the probability of the gate being active